HONEYCOMB CUL-DE-SAC HOUSING

People like to live in cul-de-sacs. According to an American study by Eran Joseph in 1995, between the ‘grid’, ‘loops’ and cul-de-sacs, the latter were the most popular. In Malaysia, a developing country with per capita income a quarter of that in the US, only the rich can afford to live in a single-family house located in a cul-de-sac. How can the cul-de-sac be made affordable for more people?

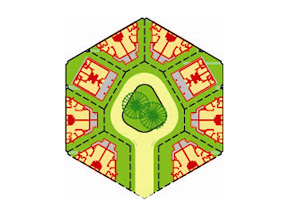
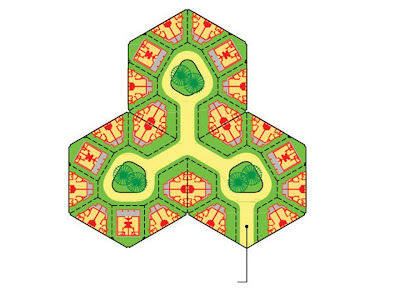
First, we improve the cul-de-sac by making it bigger to be able to fit in a public green area in the middle because local planning regulations require 10% of any residential development to be open space. Then we create an interlocking arrangement of cul-de-sacs such that each building lot would face at least two cul-de-sacs. If the buildings in this layout were detached houses, they would be in the top range of the market. In Honeycomb housing, we sub-divide the buildings into 2, 3, 4 or 6, to create duplex, triplex, quadruplex or sextuplex units. As we divide the buildings, the land area and the built-up area become smaller; the number of units in the layout and the density of the development go up. The standard of finishes of the units can also be reduced. All these make the housing units less expensive. Yet every building still retains a public access. Furthermore, the quality of the external environment is not compromised – only that more units share it!

There are two essential parts to Honeycomb housing: first is the design method which is based on the geometric concept of tessellations; second, is the re-interpretation of the idea of ‘neighborhood’, that is at present still strongly influenced by the ‘neighborhood unit’ concept, first introduced in 1929 by a sociologist, Clarence Perry, in the US.



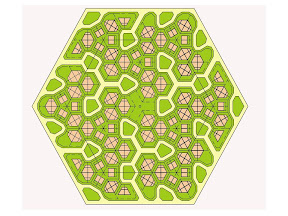
Honeycomb housing adopts a hierarchical concept of neighborhood. A family may belong simultaneously to a ‘courtyard neighborhood’ (of say, 16 houses), a ‘cul-de-sac neighborhood’ (of say, 42 homes), a ‘block neighborhood’
(250 houses, say), and a ‘town community’ of around 1500 houses. The latter is what corresponds most closely to Perry’s neighborhood unit.

However, we argue that it is at the level of the ‘courtyard neighbourhood’ that the sense of neighborhood would be strongest: a cluster of 16 houses with a population of only 80 is a setting where residents can easily relate to each other.

In this series of blogs, I will expand on this basic Honeycomb concept and show how it has been used to develop new types of houses and new forms of neighbourhood layout and urban design.

TESSELLATION PLANNING

In geometry, to tessellate means to cover a plane with a pattern without having any gap or overlap. For centuries artists and craftsmen have used tessellation as a tool to create visual effects on surfaces. Tiling is the most common form of tessellation, and in its simplest form the tiles are regular polygons.

The Muslim craftsmen in Spain in the 15th century created beautifully complex visual effects by tessellating a small basic tile pattern. Intricate and complex designs can be built up from basic tile patterns in a simple way by this process.





Looking at the example shown above, we may think it a difficult task to lay the multiple shapes of tiles. The nine pointed star, the four pointed, the spear head, the leaf like, etc. But in fact the seemingly complex pattern is built up simply by tiling a single basic square pattern. In tessellation planning this creative power is applied to town planning, where the colours are not merely decorative but represent functional space.



Below is a demonstration how the a house, its front and backyard, and a portion of the road and park fronting it, are represented in a simple triangle (1). This basic triangle comprising the house is tessellated to form a cluster of six houses.

The six houses are in turn arrayed to form a block of of thirty houses. Here, the pattern adjusted to allow for an access road into the central cul-de-sac and for bigger houses at one corner.




This block is further tessellated to form a neighbourhood of 250 houses.



The word geometry comes from the Greek "geometria", which literally means to "earth measurement". Sub-dividing land according to ownership and use was perhaps the first use of geometry, so the application of tessellation in this field is quite apt.

DESIGNING NEIGHBORHOODS

The first essential part to Tessellation Planning the design method; the second is the re-interpretation of the idea of ‘neighborhood’. We will try to explain how these two parts work together by going through the process of designing a housing layout step by step.

We start by drawing the layout of a single cluster of houses on a hexagonal ‘tile’. This is a small community of, in this example, 16 houses. All the houses face the common garden in the middle of a looping road. There is a clear boundary which is the party wall and fence that runs across the back of the houses. There is only one road leading into this cluster. Because the area in the middle of the houses forms a sort of courtyard, we call this arrangement a ‘courtyard neighborhood’. Across the courtyard is only about 150 feet. Within this distance, someone standing at his front garden would be able to make out the facial features of other people outside.



With a population of about 80 persons (based on 5 persons per unit), it is possible for a resident to at least recognize most of his neighbors. He would be likely to know when a stranger strays into this intimate setting. So here we have a ‘courtyard neighborhood’ on a hexagonal tile.

The next step is to combine three almost identical tiles together. Here we have 36 houses in a ‘cul-de-sac neighbourbood’ with a population of 180 persons. This is a bigger neighborhood, less intimate, less focused, but still defined by a single entry. The population of this area is not much higher than ……‘the figure 150 (that) seems to represent the expected maximum number of individuals with whom we can have a genuine social relationship, the kind that of relationship that goes with knowing who they are and how they relate to us… it’s the number of people you would not feel
embarrassed about joining uninvited for a drink if you happened to bump into them in a bar’ (Robin Dunbar in "Grooming, Gossip and the Evolution of Language").

The hexagonal tiles that we have been working with can be tiled further to create a ‘block neighborhood’ of about 15 acres. There are about 250 houses in this example bounded by a distribution road. At the edges are some courts, which are the cul-de-sacs courtyards dissected into two. A central park for older children is provided in the middle of the block. This open area also allows footpaths to run from one cul-de-sac to another. The population here would be about 1250.

A further step would be to create a bigger community equivalent to 7 of the block neighbourhoods described above to form a township. The residential areas are arrayed around a central area that comprises a primary school and other communal amenities. The number of houses, about 1750 units, and the population is 8750 persons. This is the community size that accords with the term "neighbourhood unit" that is normally used by planners.

In Honeycomb housing, we adopt a hierarchical concept of community - with neighbourhoods at the level of coutyards, cul-de-sacs, blocks, and township. And community planning should start at the bottom of this hierarchy, at the first cluster of houses, because that where it is most important

HONEYCOMB BUILDING TYPES

THE DUPLEX HOUSE
A residential block is divided into two units, linking back to back, each house accessed from a separate cul-de-sac. Viewed from the courtyard in front of a duplex, the house looks like a detached house.



THE TRIPLEX HOUSE
A block is partitioned into three units,whereby each unit gains access from seperate courtyards. Looking at the front of these houses, they look like detached homes.


THE QUADRUPLEX HOUSE
A residential block is divided into four units, each house having an independant accesss. Two houses face one courtyard, and the other another pair. From each courtyard the houses give the impression of being semi-detached houses shoulder-to-shoulder to each other.



THE SEXTUPLEX HOUSE
Six houses are linked tgether in a Y-formation such that two houses face each of three courtyards. Like the quadruplex, the sextuplex houses also give the impression of being semi-detached houses.



A Honeycomb layout consisting of quadruplex and sextuplex houses can yield up to 14 units an acre, making it equivalent to terrace houses.

IMPROVING LAND-USE EFFICIENCY

A terrace can be seen as a row of houses surrounded by roads. In contrast, honeycomb houses surround the road. It is easy to understand intuitively that roads accessing internally are more efficient than roads accessing houses from the external boundary. This accounts for the efficiency of cul-de-sacs.




Given a fixed area and number of houses to access, the shorter the cul-de-sac, the less the area taken up by the road. A square cul-de-sac neighbourhood has less road area than a long rectangular one. A circular one by itself would be the most efficient.








However, the circle does not tessellate. But hexagonal neighbourhoods interlock without gap or overlap.

The second consideration is the length of the distribution roads that encircle a precinct. The perimeter of a hexagonal precinct is 7% shorter than the perimeter of a square one of the same area.

The third factor is the shape of the individual lot and its effect on the buildable footprint after taking account of setback requirements. In the example shown, the truncated triangle shape of 6000 square feet yields a higher plinth area compared to a typical 60’ x 100’ site.












All of the above factors combine in honeycomb housing to produce greatly increased efficiency of land use.

We compared two theoretical sites. An efficient layout of terrace houses on an island site is compared with an equivalent honeycomb alternative.





Here again, the honeycomb alternative produces less roads and more residential land). In this example, the public green area and density (units per acre) are kept the same; consequently, the average lot sizes are 30% larger.